Using playing cards to store hidden data:

The implied card method for
encoding data into playing cards

The Basic Implied Card Method

Here I will explain the actual method for hiding binary data in decks of playing cards. This method involves having a set order for a pack of cards. Each card's position in the pack represents a 1 or 0. If the card is absent from its position, there is an implied 0; if the card is present, it represents a 1. As we know the order of the pack, we can tell if a card is absent. To encode the 4-bit binary number 1011 (eleven in decimal), we proceed as follows:

First, we lay out the cards in order:


Then we take out the card that will represent the zero, and leave the cards that will represent 1s:


Despite the card no longer being there, we know that it should be there because the cards were in order when we started:


The absent card is put at the back of the pack and will be used again when it comes around the next time. We will know the order of that part of the pack when it does come around again because we know which cards were removed the first time around and the order in which they were removed. Therefore, we can carry on with this method of keeping ones in position and putting zeroes at the back of the pack until we have run out of cards to use.


By passing absent cards to the back of the pack and using them again, it allows us (usually) to encode far more than 52 bits of data.

The method is most easily explained with an in-depth example. Choose an order for a pack of cards that you will stick with. I use aces to kings for each suit, in the order of spades, clubs, hearts, and then diamonds.



In this example, I will be encoding into the cards all the 4-bit binary numbers, in order, from 0001 to 1111. These are the binary equivalents of the decimal numbers: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14 and 15. We could just as easily encode 2-bit, 3-bit, 5-bit numbers etc, or just a string of unrelated ones and zeroes.

We lay out the cards face up, in order, on a large table or the floor in groups of four. Then, starting at the beginning, we will convert the cards into the binary equivalent of the number we want them to represent. The first number will be 0001, so we remove the first, second and third cards and leave the fourth. In other words, the only card left of that group will be the 4 of spades. The removed (absent) cards (ace, 2, and 3 of spades) are put in order at the end of the whole set of laid out cards (i.e. after the king of diamonds).

Next, we want 0010 (2 in decimal). Therefore, we remove the first, second and fourth cards from the next group of four cards, while leaving the third in place. This leaves the 7 of spades. The removed cards (5, 6, and 8 of spades) are put in order at the end of the laid out cards. [When we get to the back of the pack, the removed cards can be used to form groups of four themselves.]

For the next group of four, we want 0011 (3 in decimal). Therefore, we remove the first two cards, and leave the second two cards. The remaining cards are the jack and queen of spades.

We continue like this until, eventually, we have been through the entire pack once. At this point, we will be once more at the ace of spades, which on the first run represented a zero, so was removed as an absent card. When we are at this point in the pack, we will be about to encode the binary number 1110 (14 in decimal). The cards that we removed and passed to the back of the pack have a new set position and order. Where they are, and where they should be, can be worked out from the fact that they were absent before. Therefore, the Implied Card Method will continue to work here, and it will continue to work all the way through until we have no more cards to use.

We will continue with our encoding of 1110 into the group of four previously removed cards (the ace, 2, 3 and 5 of spades). We keep the first three cards and take out the fourth (the 5 of spades). We put the removed 5 of spades at the end of the pack of laid out cards as before. The next number is 1111 (15 in decimal), which is the highest number we can represent with 4 bits. The cards in this group are the 6, 8, 9 and 10 of spades. We keep them all. We could stop here, but instead, we will reset our counter and continue encoding into this pack. To make things different this time, we will start at 0000 (zero) and count up from there. The next group of four in the pack consists of the king of spades and the 2, 3 and 4 of clubs. As our number is 0000, we take all four cards, and put them all at the back of the pack. One of the oddities of this method is that zeroes do not actually use up any cards. All those four cards will be used to encode further numbers in this pack when they come round again next time. I will explain more about this later, but for now, we will continue counting. Our next number is 0001. The cards in the associated group of four are the 6, 8, jack, and queen of clubs. We put the 6, 8 and jack at the back and keep the queen.

We continue counting until, eventually, we will run out of enough cards to encode a 4-bit number. The second-last 4-bit number that we can do is 1001 (9 in decimal). The cards are the 3 of clubs, the 6 of clubs, the 4 of hearts, and the 5 of hearts. We keep the 3 and the 5, and we put the 6 and the 4 at the back of the pack. When we are at the very last number, 1010 (ten in decimal), there will be the queen of diamonds, the 5 of spades, the king of spades and the 6 of clubs. The 5 and the 6 go to the back of the pack, and we keep the queen and the king.

At this point, there are only three cards left. It is sometimes possible to encode a 4-bit number with three cards if there are enough zeroes in it, but to keep this example simple, we will stop here. The remaining cards, in order, are the 4 of hearts, the 5 of spades, and the 6 of clubs.

If you are trying this yourself, then comparing the remaining cards in this and the following examples can help you see if your encoding was correct, or if you made any mistakes. The remaining cards are equivalent to a very half-hearted checksum. There will be many different encodings that will produce the same leftover cards. However, you can be sure that if your last cards are different then you (or I) have made a mistake somewhere.

At this point, the sequence of binary numbers is completely encoded within the sequence of the cards. Pick up the laid out cards in order that we went through them, so the first card is face up at the top of the pack, and the last card (the 6 of clubs) is face up at the bottom of the pack. Including the final unused "meaningless" cards keeps all 52 cards together, and won't confuse matters, as long as the person decoding them knows the context behind what has been encoded. The remaining cards, if left in order, will all represent ones when decoded, and it will usually be clear that the message has ended.

Once you understand the encoding method, laying out the cards on a table or the floor is not really necessary, and you can sort them in your hands to save the trouble of picking them all up afterwards. Laying the cards out just made it easier to see what we were doing.

Counting from 0001 to 1111 and then from 0000 to 1010 means we can represent 26 4-bit numbers (104 bits) in 49 cards with 3 cards left over. Other more simple methods would only get 13 4-bit numbers (52 bits) with a pack of 52 cards. My method achieves a better bit-per-card ratio because the absent cards that represent zeroes are put to the back of the pack and used again. In the above example, the five of spades and the six of clubs are "absent" five times, and so act as zeroes in five different 4-bit numbers. The more zeroes there are in the binary numbers involved, the more cards we can use several times, so the more numbers can be represented with just one pack.




As we saw, the number 0000 doesn't actually use any cards. All the cards are passed to the back of the pack. This is one of the paradoxes of this method - some numbers can be encoded without reducing the number of cards available for encoding other numbers.

Despite the encoding of a zero not actually using any cards, there is a limit to the number of repeating zero numbers that we can use. We could not have a million 0000 4-bit numbers with 52 cards. At some point, the cards that get to the back of the pack would end up in exactly the same order and position as at the beginning of the encoding. There would be no difference to the pack if the zeroes had never even been encoded, and when the cards are decoded, the numbers wouldn't appear. An uninterrupted string of zeroes becomes invisible when there is the same number of zeroes (or more) as remaining cards to be used for encoding. To stop zeroes becoming invisible, there needs to be at least one "one card" in the pack after the place where the "zero cards" are being put.

If a whole pack is being encoded with zeroes, then, for 4-bit 0000s, the consecutive zeroes will become invisible when all 52 cards have been used, which happens after thirteen 4-bit numbers have been encoded. The maximum number of consecutive 4-bit 0000s encodable in a full pack is 12. After the thirteenth number, the pack is in exactly the same order as it was to start with, so there is no way of telling if there are 52 absent cards or none at all. For zero numbers made up of say 3-bits or 5-bits (i.e. that aren't a neat divisor of 52), when the pack wraps around, it will be impossible to tell if there is a whole string of zeroes or some other valid number instead. Eleven 5-bit 00000 numbers in a row would end up with the bits 00011 appearing at the start of a pack. This would be decoded as the number 3, which not only means the zeroes are all invisible but that we have started decoding nonsense.

It makes sense to be aware of this potential pitfall. If you are about to encode a very long string of zeroes, always make sure that there will be at least one "one card" before you reach the end of the cards in the rest of the pack.




To decode a pack of cards, we first write out the names and suits of the cards in order in a row across the top of a piece of paper:


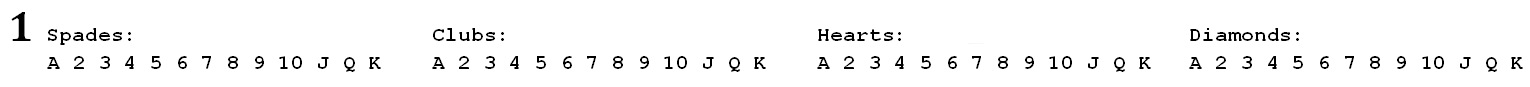
Or, if that picture is too small to see:

Spades: A 2 3 4 5 6 7 8 9 10 J Q K; Clubs: A 2 3 4 5 6 7 8 9 10 J Q K; Hearts: A 2 3 4 5 6 7 8 9 10 J Q K; Diamonds: A 2 3 4 5 6 7 8 9 10 J Q K.

I will be calling this a "Decoding Row" because it is a row, and it helps with decoding.

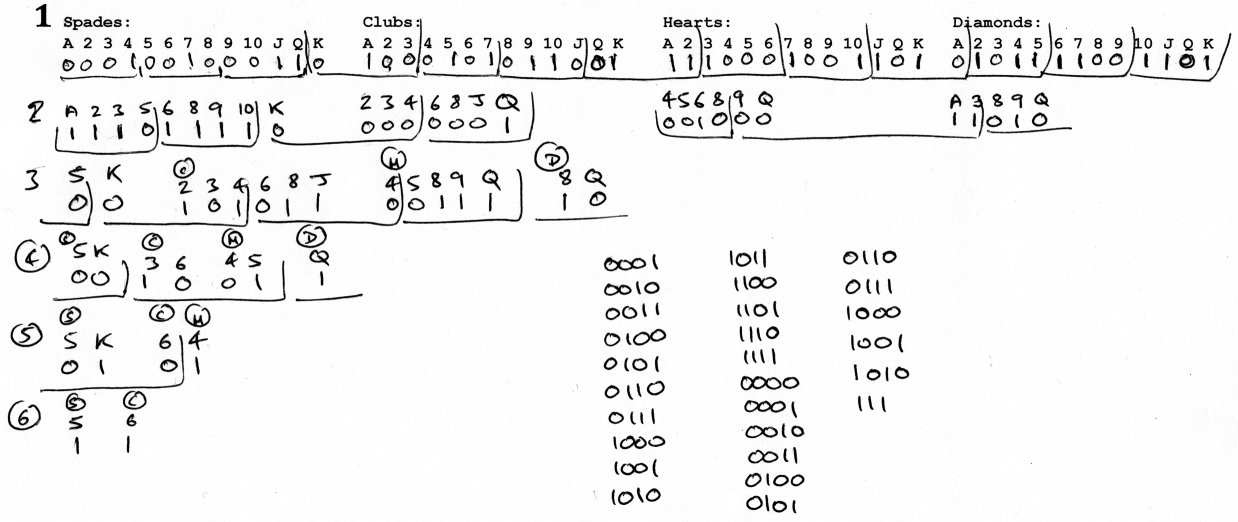
Looking at this "Decoding Row", we go through the pack of cards in order from the start one by one to see which cards are absent and which are present. We write a 0 under the entries for cards that are absent, and a 1 for cards that are present. In our example, the first card in the pack is the 4 of spades. Therefore, the ace, 2 and 3 are absent, so we put a 0 under their entries in our row, and a 1 under the 4 of Spades. The next card is the 7 of spades. We put a 1 underneath that, and put a zero underneath the 5 and 6 because they are absent. Next, we have the jack of spades. We put a 1 underneath that, and we put a zero under each of the 8, 9, and 10 of spades. Then the queen of spades is there, so we put a 1 underneath that. The next present card is the ace of clubs. We put a 1 underneath that, and a 0 underneath the preceding absent king of spades.

We continue like this until we get to the end of our row - it ends with the king of diamonds, which has a 1 put underneath it because the card is present.

We then write a new Decoding Row underneath the first one, but this one will just contain the cards that were marked with a zero in the first row - the absent cards. Make sure to include the suits in your row to avoid confusion. In this particular example, the new Decoding Row will look like this:

Spades: A, 2, 3, 5, 6, 8, 9, 10, K; Clubs: 2, 3, 4, 6, 8, J, Q; Hearts: 4, 5, 6, 8, 9, Q; Diamonds: A, 3, 8, 9, Q.

It is very easy to make mistakes decoding the pack, but it is not too much effort to correct them.

Once we have written out the second Decoding Row, we go through it and mark a 1 or 0 underneath each entry depending on whether it is there or not. We put a 1 underneath the ace of spades, the 2 and the 3. The 5 of spades is absent, so we put a zero underneath it. The six is present so it gets a 1, and so on. In this example, only one club gets a 1 written underneath it in this row.

At the end of the second row, we reach the queen of diamonds, which is absent so receives a 0. We then start a third row containing a list of the cards that were absent in the second row. In our example, this will be as follows:

Spades: 5, K; Clubs: 2, 3, 4, 6, 8, J; Hearts: 4, 5, 8, 9, Q; Diamonds: 8, Q.

We continue marking the 1s and 0s, and creating more rows and going through them until we have gone through all the cards. In this example, there are six Decoding Rows needed, although the last one only has two cards in it (the 5 of spades and the 6 of clubs) and those cards do not have any meaning attached to them. Likewise, the 4 of hearts at the end of the previous row has no meaning.

We can now read off the binary numbers that were originally encoded in the cards by reading the ones and zeroes in the rows in order. If we did not make any mistakes, the numbers will be identical to the ones we originally encoded, and we will have successfully decoded the hidden data. The last three cards will be 1s, but we know to ignore them.





If there happened to be more 1s than 0s in the string of binary that we were encoding, then it would make sense to have 1s as the absent cards, and keep the 0s. This would mean more cards would be available to be reused. The person decoding the data would need to know that this had been done, although they might be able to work it out by the context of the numbers involved. We will ignore this optimisation here, as it will just confuse the explanations.




One of the problems with the encoding method is that cards that are not used at the end of the pack will become decoded as 1s. This might be confusing if the person who is decoding the pack does not know the length of the message or its likely contents. Supposing our data consisted of only 40 bits, which were all 1s, when the pack is decoded, we would have another 12 bits of 1s.

Ways to solve the problem:
1: We could mark where the data ends with a joker, by turning the extra cards backwards, or by slipping bits of paper in. This is a simple and certain way to indicate where the data ends. It would also be possible to crease the corner of a card, but that would mean the pack could only be used once. A downside to these solutions is that they make it more obvious that the pack contains data. Besides that, when we get on to the Recursive Method, we will need the Jokers for another purpose.

2: We could work with known bit sizes of numbers rather than individual bits. If the person encoding and the person decoding both know that they are working with 4-bit numbers, and there are three cards left at the end of the pack, then the decoder will know they cannot be part of our number and are just unused cards. This would solve the problem of a few unused 1s, but would not work for a large number of them.

3: We could work with fixed-length numbers. If we only ever encoded 128-bit numbers, we could stop decoding once we had decoded 128 digits.

4: We could use escape characters. In other words, we could use a particular encoding of bits to indicate that the next bits were a genuine set of 1s. If we were encoding 4-bit numbers, the escape character could be something like 0100. Every time 0100 preceded 1111 we would know it was a genuine 1111 and not the end of the pack. This, of course, creates the problem of how to encode 0100 when we need to. We could solve this problem by putting "genuine" 0100s in a pair, so 0100 0100 always means "0100", while 0100 1111 always means "1111". The downside to this solution is that it slightly reduces the amount of useful data that we can store in a pack.

I will ignore the "final one problem" in this explanation to keep things simple.

Previous page    Next page